En el mundo de las matemáticas y la informática, los grafos son una herramienta esencial para representar relaciones entre objetos. Aunque a simple vista puedan parecer conceptos abstractos, tienen múltiples aplicaciones prácticas. Desde la planificación de rutas hasta las redes sociales, los grafos están presentes en numerosas áreas de nuestra vida cotidiana.
Definición de grafos
Un grafo es una estructura compuesta por nodos (también llamados vértices) y aristas (o enlaces) que conectan estos nodos entre sí. Esta estructura permite modelar relaciones, caminos y conexiones de una forma visual y lógica. En otras palabras, un grafo es una representación que facilita el análisis de sistemas complejos.
Los nodos representan entidades, mientras que las aristas representan relaciones entre esas entidades. Por ejemplo, en un grafo que modela una red de transporte, los nodos serían las estaciones o ciudades, y las aristas serían las rutas o carreteras.
Tipos de grafos
Existen diversos tipos de grafos, y cada uno se adapta a necesidades diferentes. Conocer sus variaciones permite aplicar el modelo más adecuado según el problema que se desee resolver.
Grafos dirigidos
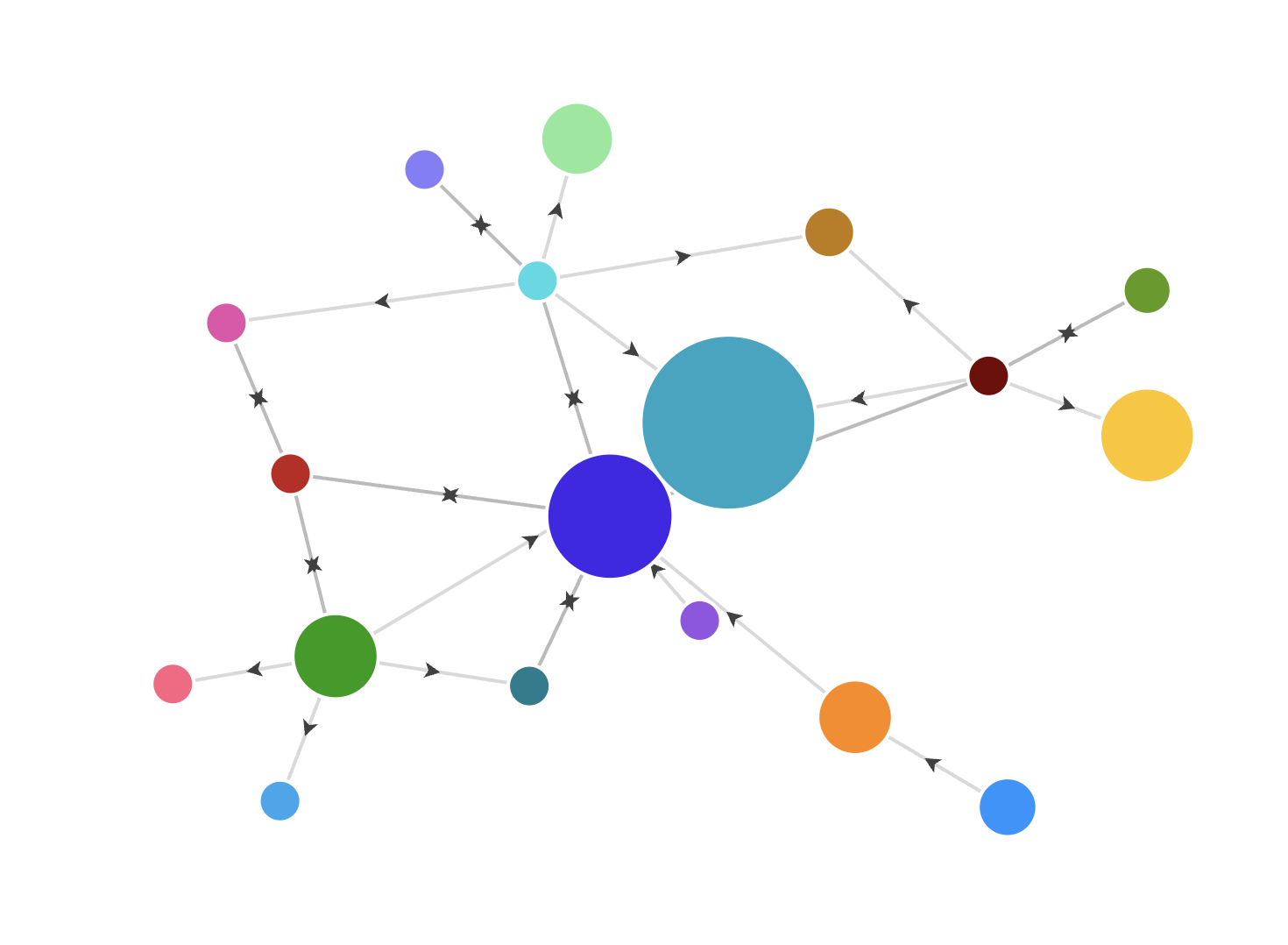
En un grafo dirigido, las aristas tienen una dirección. Es decir, la conexión entre dos nodos no es simétrica. Este tipo de grafo se utiliza, por ejemplo, en flujos de trabajo o diagramas de procesos, donde el orden importa.
Grafos no dirigidos
A diferencia del anterior, en un grafo no dirigido las aristas no tienen dirección. Esto significa que la relación entre los nodos es bidireccional. Este tipo de grafo es común en redes sociales, donde una amistad suele ser recíproca.
Grafos ponderados
Algunos grafos incluyen pesos en sus aristas. Estos valores numéricos representan la intensidad, el costo o la distancia de la relación entre nodos. Por tanto, los grafos ponderados son ideales para problemas como encontrar el camino más corto entre dos puntos.
Grafos cíclicos y acíclicos
Un grafo cíclico contiene al menos un ciclo, es decir, un camino que comienza y termina en el mismo nodo. En cambio, un grafo acíclico no tiene ciclos. Los grafos acíclicos dirigidos (conocidos como DAGs, por sus siglas en inglés) se usan comúnmente en análisis de dependencias o en estructuras jerárquicas.
Aplicaciones de los grafos
El uso de los grafos va mucho más allá del ámbito teórico. En realidad, tienen una amplia gama de aplicaciones en distintos sectores. Veamos algunas de las más relevantes.
Ciencias de la computación
Se utilizan extensamente en algoritmos, bases de datos, inteligencia artificial y redes. Por ejemplo, en algoritmos de búsqueda como Dijkstra o A*, el grafo es fundamental para encontrar rutas óptimas.
Redes sociales
Cada usuario de una red social puede ser representado como un nodo, y cada relación como una arista. Esta representación permite analizar patrones de comportamiento, influencia o difusión de información entre usuarios.
Biología y química
En estas disciplinas, los grafos se emplean para modelar estructuras moleculares, redes neuronales o cadenas alimenticias. Gracias a los grafos, se puede estudiar la interacción entre diferentes elementos de un ecosistema o de un sistema biológico.
Logística y transporte
El diseño de rutas óptimas, la gestión de tráfico y la distribución de mercancías se benefician del uso de grafos. Además, permiten simular posibles escenarios y prever problemas antes de que ocurran.
Representación de los grafos
Los grafos pueden representarse de diversas maneras, según las necesidades del análisis. Dos de las formas más comunes son:
Matriz de adyacencia
Es una matriz cuadrada donde cada fila y cada columna representan un nodo. Las celdas indican si existe una conexión entre los nodos correspondientes. Aunque esta forma consume más espacio, permite comprobar conexiones rápidamente.
Lista de adyacencia
En este caso, cada nodo tiene una lista que contiene los nodos con los que está conectado. Esta representación es más eficiente en términos de espacio, sobre todo cuando el grafo tiene pocas aristas en comparación con el número de nodos.
Algoritmos sobre grafos
El estudio de los grafos no estaría completo sin mencionar los algoritmos que permiten analizarlos y resolver problemas complejos. Algunos de los más importantes incluyen:
-
Algoritmo de Dijkstra: Encuentra el camino más corto desde un nodo de origen hacia todos los demás nodos en un grafo ponderado.
-
Algoritmo de Kruskal: Construye un árbol de expansión mínima, es decir, una forma de conectar todos los nodos con el menor costo total posible.
-
Algoritmo de búsqueda en profundidad (DFS) y búsqueda en anchura (BFS): Permiten recorrer todos los nodos de un grafo de manera sistemática, útil para analizar su estructura o encontrar componentes conectados.
En resumen, los grafos son herramientas poderosas que permiten modelar y resolver problemas complejos en una amplia variedad de contextos. Aunque su concepto pueda parecer abstracto al principio, su aplicación práctica es indiscutible. Desde redes tecnológicas hasta sistemas biológicos, los grafos ofrecen una manera estructurada y eficiente de entender cómo se conectan y relacionan los elementos en un sistema. Por esta razón, se han convertido en un pilar fundamental dentro de muchas disciplinas científicas y tecnológicas.